Track: Python devroom
Room: H.1308 (Rolin)
Day: Saturday
Start: 11:30
End: 12:00
(me too, I love to have the slides during presentation so here is the url
http://jul.github.io/cv/pres.html)If you behave nicely and consistently you have super cow powers including
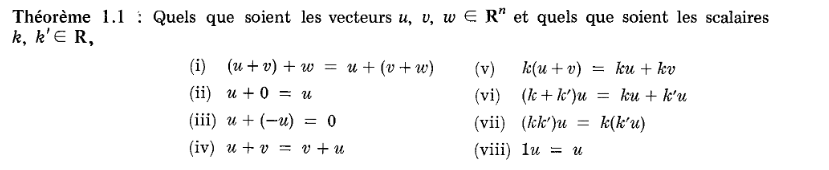Nota Bene:
Doesn't it look like the exact perfect match case of a unit test?
Consistent Algebra test
**************************************************
testing for 'complex' class
a = (1+0j)
b = (1+1j)
c = (1-4j)
an_int = 2
other_scalar = 3
neutral element for addition is 0j
**************************************************
test #1
a + b = b + a
'test_commutativity' is 'ok'
test #2
a + neutral = a
'test_neutral' is 'ok'
... other tests ....
test #12
an_int ( a + b) = an_int *a + an_int * b
'test_distributivity' is 'ok'
**************************************************
14/14
<type 'complex'> respects the linear algebrae standard rules
**************************************************
| Type | Neutral of add. | Neutral of mul. | Result |
|---|---|---|---|
| Numpy array | zeroes(dim) | ones(dim) | OK |
| floats | 0.0 | 1.0 | OK |
| int | 0 | 1 | OK |
| Decimal | Decimal(0.000000) | Decimal(1.000000) | KO |
| complex | 0+0j | 1+0j | OK |
| list | [ ] | 1 | KO |
Yes, math rox, you are free to code whatever you want and you don't have to justify youself, as long as you pass the tests
Note: it has nothing to do with coconut/rust algebraic data type as explained on wikipedia. I would say, if I would understand it.
On a MutableMapping anything that is not a leaf is a part of a key.
But let's turn
{ 'a': { 'b' : 1 }, 'b' : 2}
AS
{ ('a', 'b') : 1; 'b': 2 }
All keys are immutable. So the tuple of the keys is also...immutable.
Hence:
Every distinct immutables path to a value are a key, and
then we can reduce a recursive problem to a 1 level problem.
All MutableMapping are utimately possibly put in a canonical one level form.
Every distinct immutable paths to a value are equivalent to a dimension.
We have an isomorphism between the one level MutableMapping and arbitrary depth MutableMappings.
Arbitrary choices:
__neg__ = lambda self: self*=-1to ensure consistency
The exact same trick can probably be implemented in C++, in ruby, Perl, PHP, javascript...
************************************************** testing for 'Daikyu' class a = {'one_and_two': 3, 'one': 1} b = {'two': 2, 'one_and_two': -1} c = {'one': 3, 'three': 1, 'two': 2} an_int = 2 other_scalar = 3 neutral element for addition is {} ************************************************** ... 16 tests later ... ************************************************** 16/16Yes!!!respects the linear algebrae standard rules **************************************************
from collections import MutableMapping MARKER=object() def paired_row_iter(tree, path=MARKER): if path is MARKER: path = tuple() for k, v in tree.iteritems(): if isinstance(v, MutableMapping) and len(v): for child in paired_row_iter(v, path + (k,)): yield child else: yield ((path + (k,)) , v) dict(paired_row_iter({ 'a' : { 'b' :1}, 'c':2, 'd' : {'e': []}, 'e': {} }) ) # {('a', 'b'): 1, ('c',): 2, ('d', 'e'): [], ('e',): {}}
dot = lambda u,v: sum(v for i,v in paired_row_iter(u*v)) dot(mdict(x=1,y=1, z=1), mdict(x=1, y=1, z=1)) # 3 dot(mdict(x=1,), mdict( y=1, z=1)) # 0 dot(mdict(x=1,), mdict(x=-1, y=1, z=1)) # -1For int and real, the resutls are following expectation.
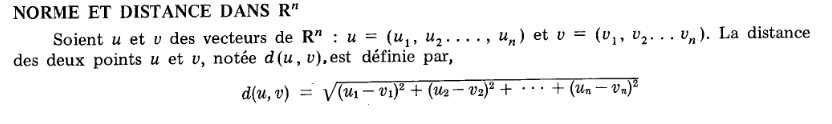Now we can define abs (which is a mathemtic shortcut for L2 distance/norm) and distance as
vabs = lambda v: dot(v,v)**.5 distance = lambda u, v: vabs(u-v)It would be more aesthetic for vector of dimension p to write. $$ \left\| x \right\| _p = \bigg( \sum_{ i \in \mathbb N} \left| x_i \right| ^p \bigg) ^{1/p}$$
vcos = lambda u,v : dot(u,v) / vabs(u) / vabs(v) vcos(mdict(x=1, y=1), mdict(x=1, y=0)) # Out[27]: 0.7071067811865475 2**.5/2 # Out[29]: 0.7071067811865476 (cos(45°) vcos(mdict(x=1, ), mdict(x=2, y=4, z=4, v=4)) # Out[30]: 0.3333333333333333 (cos 60°) vcos(mdict(x=1), mdict()) # ZeroDivisionError: float division by zeroSo far so good.
We have something that is built for infinite intricated dimensions, and
that already works for the 2D & 3D euclidean space without even trying.
And we even have a meaningful exception: cos with a null vector does not mean a thing.
Our boring data job? Take a dict (like after we parse a log line, or cvs) and aggregating the data in a dict.
log_line = mdict( ip = "127.0.0.1", user_agent = "moz", country="BE",
url="/toto" )
data = mdict( by_country = mdict( GR=12, CA=10), user_agent=mdidct(chrome=1, ie=1000,))
data["user_agent"] += log_line * mdict( user_agent = 1)
What if we don't have a dict, but just a MutableMapping that directs __getitem__ and __setitem__ to a distant instance? 
Use a spacebar or arrow keys to navigate